本記事では、工事担任者 総合通信のうち、2024年第2回電気通信技術の基礎問3の解説を行います。

私が工事担任者 総合通信に合格した際の勉強方法等はこちらの記事をご覧ください!


工事担任者からステップアップして電気通信主任技術者を目指したい方はこちらの記事をご覧ください!


第3問
(1)
問題
解説
解:4
ベン図についての設問です。
ベン図は与えられた論理式が「1」となる部分を塗ります。
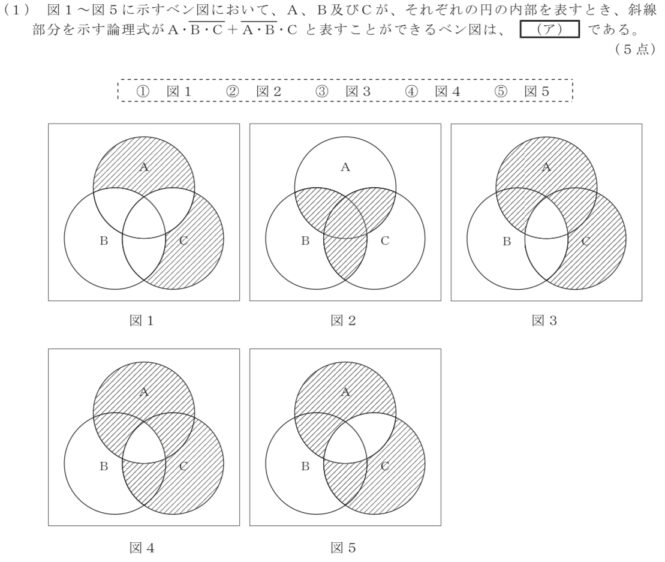
まず、\(A・\overline{B・C}\)は、言葉で表すと「Aかつ」「BとCが重なる部分以外」で、ベン図だとこのようになります。
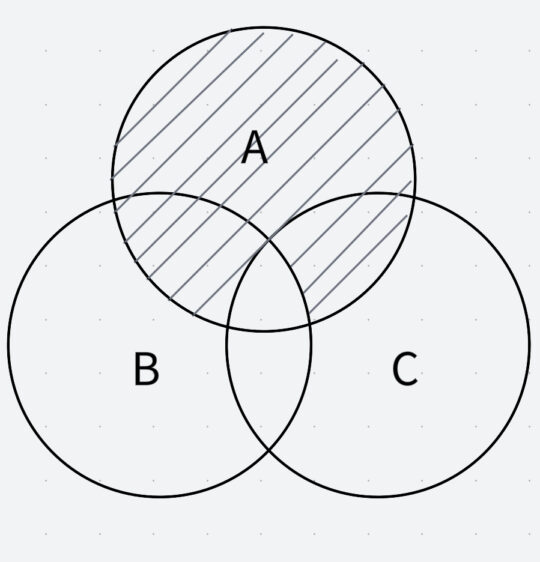
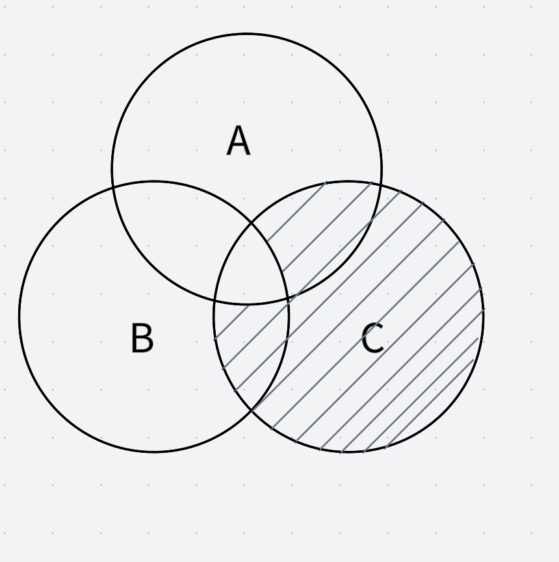
次に、\(\overline{A・B}・C\)は、以下の通り表せます。
そして、それらのORなので、色が塗られている部分を重ね合わせると、このようになります。
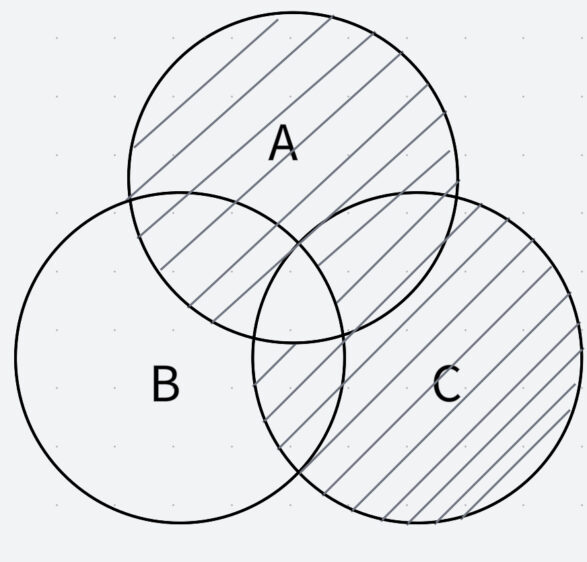
(2)
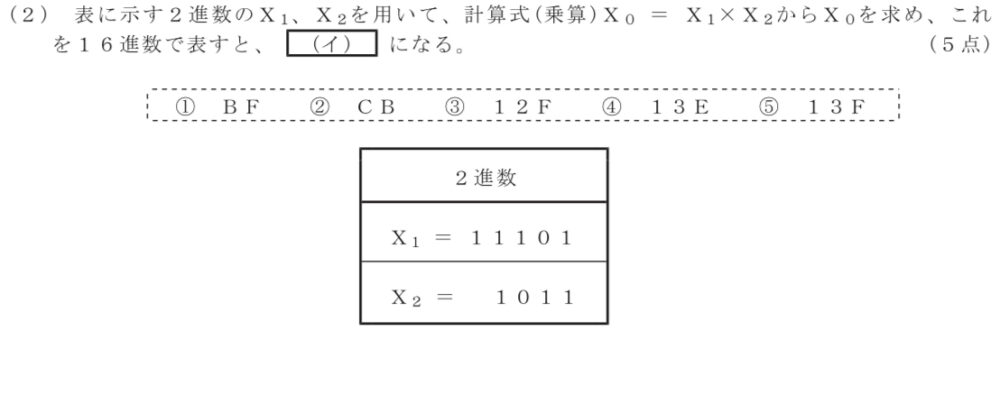
問題
解説
解:5
2進数の変換に関する設問です。
2進数の乗算は整数の乗算と同じやり方で解けます。この時、桁上がりに注意。
).png)
乗算の結果、「100111111」が得られました。次に左から4つ毎に区切っていきます。一番右側が1のみになりますが、0を3つ追加してください。
.png)
区切った①~③をそれぞれ10進数に変換します。
.png)
.png)
.png)
以上より、「1」「3」「15」が得られましたので、それぞれ16進数に変換すると「1」「3」「F」が得られます。
(3)
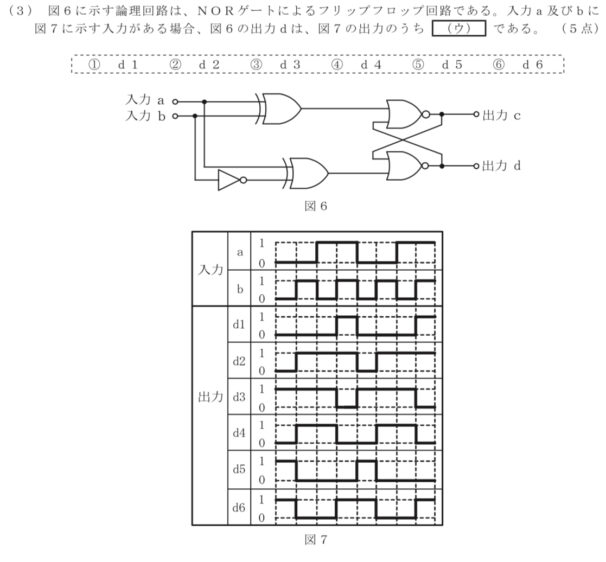
問題
解説
解:4
サービス問題です。論理回路を理解していれば、後はひたすら当てはめて合致するものを探すだけです。
論理回路については以下の通り。
【NOT回路】
入力を反転させ出力する。
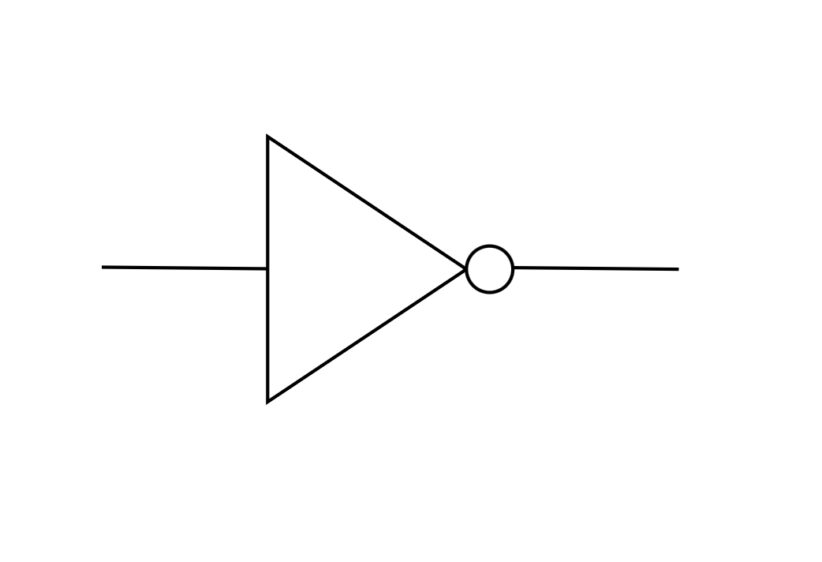
| 入力 | 出力 |
| 0 | 1 |
| 1 | 0 |
【NOR回路】
OR回路の出力を反転させたもの。
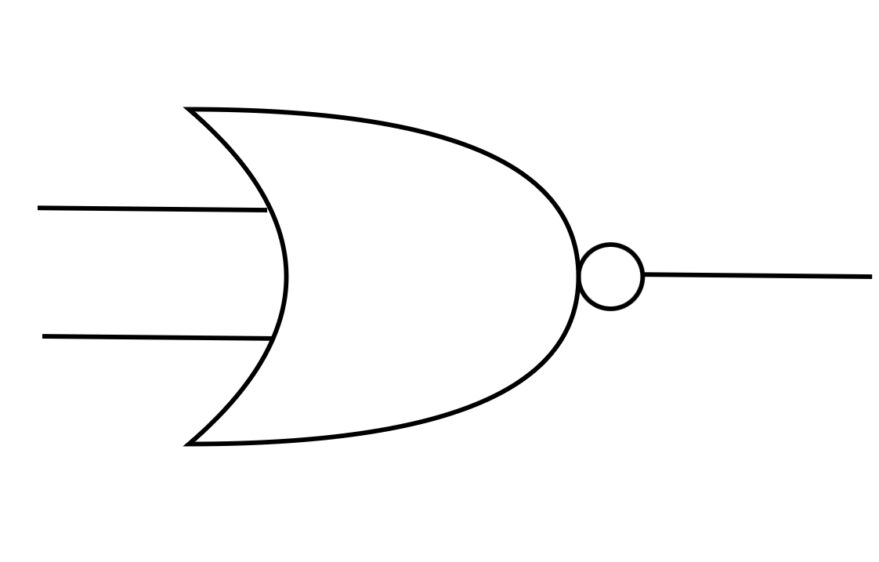
| 入力A | 入力B | 出力 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
【XOR回路】
入力が一致している時のみ出力する。
| 入力A | 入力B | 出力 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
(4)
問題

解説
解:5
括弧の中から整理します。
\((\overline{B}•(C+\overline{C})+\overline{A}•(C+\overline{C})\)
\(=\overline{B}+\overline{A}\)
次に\(A・B\)と括弧の中身を計算します。
\(A・B(\overline{A}+\overline{B}\)
\(=A・\overline{A}・B+A・B・\overline{B}\)
\(=0+0\)
なので、残り分は
\(A・\overline{B}+\overline{A}・B\)



コメント