本記事では、2024年第2回 工事担任者 総合通信のうち、電気通信技術の基礎 問1の解説を行います。

私が工事担任者 総合通信に合格した際の勉強方法等はこちらの記事をご覧ください!


工事担任者からステップアップして電気通信主任技術者を目指したい方はこちらの記事をご覧ください!


第1問
(1)
問題
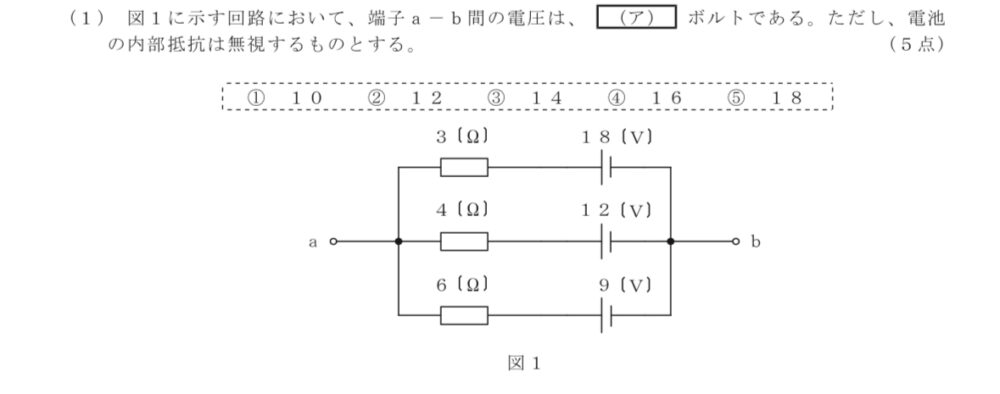
解説
解:3
【ワンポイント】
本問は、ミルマンの定理を用いて解きます。
ミルマンの定理とは、「抵抗と電圧源が直列に接続されたものを複数個並列接続した回路の解放電圧を求める」ための定理です。回路はこんなにイメージ。
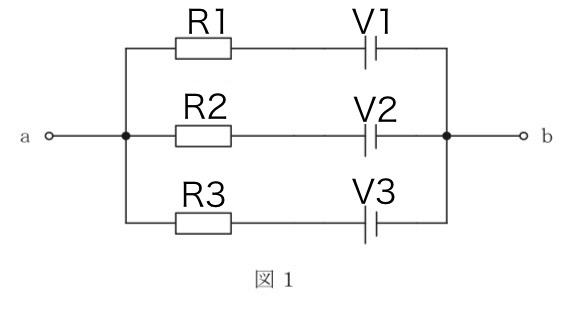
式で表すとこのようなものです。
\(\displaystyle Va-b=\frac{\frac{V1}{R1}+\frac{V2}{R2}+\frac{V3}{R3}}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}}\)
この式は必ず覚えてください。
【解法】
ミルマンの定理に値を代入してときます。題意より、R1=3Ω、R2=4Ω、R3=6Ω、V1=18V、V2=12V、V3=9V
を電源の向き(極性)に注意し、代入します。
端子a-b間の電圧Va-b[V]は、
\(\displaystyle Va-b=\frac{\frac{18}{3}+\frac{12}{4}+\frac{9}{6}}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}\)
\(\displaystyle =\frac{6+3+1.5}{\frac{4}{12}+\frac{3}{12}+\frac{2}{12}}\)
\(\displaystyle =\frac{10.5}{\frac{9}{12}}\)
\(\displaystyle =10.5\times{\frac{12}{9}}\)
\(=14\) [Ω]
以上より、③が答えとなります。
(2)
問題
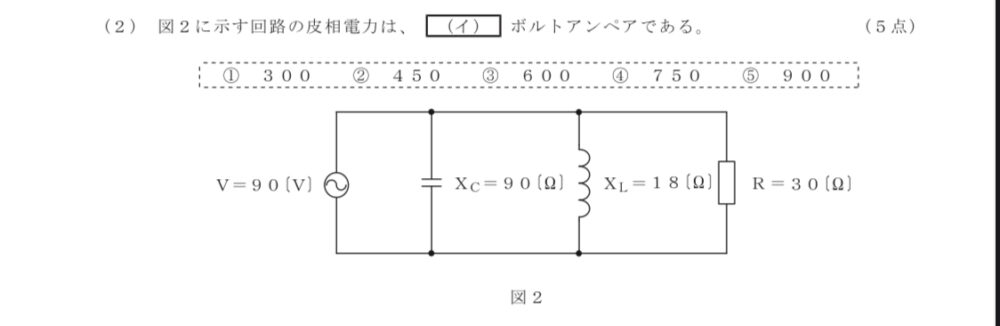
解説
解:2
【ワンポイント】
交流回路の基本的な計算をマスターしましょう。
・オームの法則
\(\dot{V}=\dot{Z}\times\dot{I}\) [V]
・合成インピーダンス
\(\dot{Z}=R+j\dot{X_L}-j\dot{X_C}\) [Ω]
・合成アドミタンス
\(\displaystyle \dot{Y}=\frac{1}{\dot{Z}}=\frac{1}{R}+j\frac{1}{\dot{X_C}}-j\frac{1}{\dot{X_L}}\) [S]
・皮相電力
\(\dot{S}=\dot{V}\times\dot{I}\) [VA]
・絶対値の求め方
\(|\dot{Z}|=\sqrt{R^2+X^2}\) [Ω]
電流なども同様の解き方で絶対値を求められます。
【解法】
合成アドミタンス\(\dot{Y}\)[S]を求めます。
\(\displaystyle \dot{Y}=\frac{1}{R}+j\frac{1}{\dot{X_C}}-j\frac{1}{\dot{X_L}}\) [S]
\(\displaystyle =\frac{1}{30}+j\frac{1}{90}-j\frac{1}{18}\)
求めた合成アドミタンス\(\dot{Y}\)[S]に電圧\({V}\)[V]を掛けて、電流\(\dot{I}\)[A]を求めます。
\(\displaystyle \dot{I}=90\times(\frac{1}{30}+j\frac{1}{90}-j\frac{1}{18})\)
\(=3-j4\)[A]
電流\(\dot{I}\)[A]から、絶対値\(I\)[A]を求めます。
\(I=|\dot{I}|=|3-j4|=\sqrt{3^2+4^2}=\sqrt{25}=5\)[A]
皮相電力\(S\)[VA]は、単位を見てわかる通り、電圧と電流の積で求められます。
従い、皮相電力\(S\)[VA]は、
\(S=V\times{I}=90\times{5}=450\)[VA]
以上より、②が答えとなります。
(3)
問題

解説
解:4
【ワンポイント】
レンツの法則とファラデーの電磁誘導の法則に関する設問です。
前半部分の「コイルに交流電流が流れると、コイル内には時間的に変化する磁束が生じ、流れる電流を妨げる向きに誘導起電力が生じる」がレンツの法則で、
後半部分の「誘導起電力の大きさ」が、ファラデーの電磁誘導の法則の説明になります。
ファラデーの法則は、誘導起電力の大きさを\(V\)[V]、巻数を\(N\)[巻]、磁束を\(Φ\)[wb]とすると、
\(\displaystyle V=-N\frac{dΦ}{dt}\)[V]
で表されます。本式を自己インダクタンスとの関係式に書き直すと、以下の式が得られます。
\(\displaystyle V=-L\frac{di}{dt}\)[V]
【解法】
「ワンポイント」より、誘導起電力は、「コイルの自己インダクタンス」と「電流の時間変化率」の積で求めることが出来ると分かります。
以上より、④が答えとなります。
(4)
問題

解説
解:5
物質は原子核(+)と電子(-)から構成されています。
さらに物質は、電子が原子核に拘束されずに自由に動ける度合いから、大まかに、「導体」「半導体」「絶縁体」に分けられます。
絶縁体は電子が原子核に強く拘束されるため、電子は自由に動きません。
そのため、設問のように正に帯電した物質を近づけると、電子が拘束状態のまま、物質側に引き寄せられ、原子核は物質と反対側に動きます。
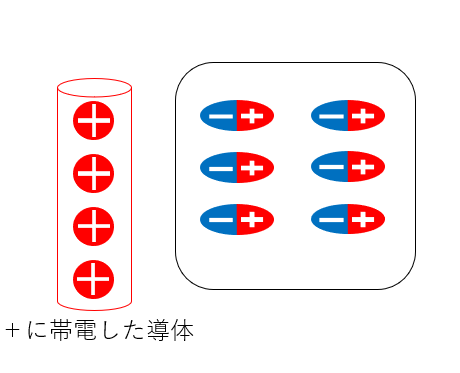
以上より、⑤が答えとなります。



コメント