【2024年第2回】工事担任者（総合通信 ）電気通信技術の基礎 問4 過去問解説

本記事では、2024年第2回 工事担任者 総合通信のうち、電気通信技術の基礎 問4の解説を行います。

一発合格出来た！オススメ勉強法！工事担任者(総合通信)

なかまるこんにちは、なかまるです！今回は工事担任者(総合通信)について、私が一発合格できた時の勉強方法について、紹介します！私の経歴についてはこちらをご覧下さい♪過去問解説については、こちらをご覧ください。こんな方におすすめの記事工事担任者...

denkiwohimotoku.com

2023.05.22

完全独学で一発合格できた！電気通信主任技術者（伝送交換）勉強方法

2023年度第2回電気通信主任技術者（伝送交換）試験に合格しました。その際の勉強方法等について解説します。

denkiwohimotoku.com

2024.03.20

【完全独学】【一発合格】電気通信主任技術者（線路）勉強方法

この記事はこんな方へオススメ！合格方法などをWebで調べても古い情報しかない。新しい情報を知りたい。過去問からほとんど出題されないのに、どうやって勉強したらいいか悩んでいる。これまで何度も受験してきたが、なかなか合格できない。受験を検討して...

denkiwohimotoku.com

2024.12.16

第4問

（1）

問題

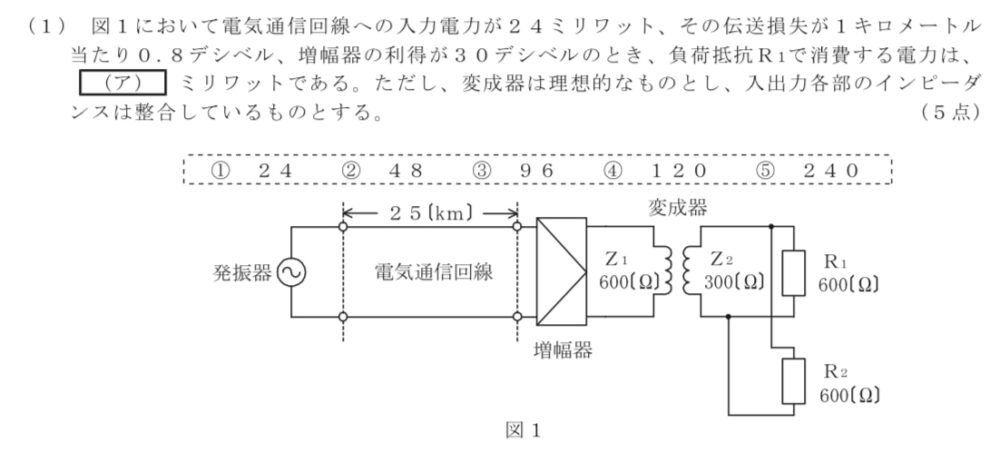
解説

解：4

対数計算が必須になります。

電力の利得\(Gp\)［dB］は、増幅器への入力電力を\(Pi\)［W］、出力電力を\(Po\)［W］とすると以下の式で表されます。

\(\displaystyle Gp=10\log_{10}\frac{Pi}{Po}\) ［dB］

まずは\(Gp\)［dB］を求めます。

題意より、「伝送損失が1Kmあたり、0.8dB」とあり、伝送距離が25Kmですので、伝送損失\(Gpl\) ［dB］は、

\(Gpl=0.8\times25=20\) ［dB］

さらに増幅器の利得が30［dB］であるため、最終的な電力利得\(Gp\)［dB］は、

\(Gp=30-20=10\) ［dB］

となります。

次に\(Po\)［W］を求めます。

前述の式に\(Gp\)［dB］を代入すると、

\(\displaystyle Gp=10\log_{10}\frac{Pi}{Po}\)

\(\displaystyle 10=10\log_{10}\frac{Pi}{Po}\)

\(\displaystyle 1=\log_{10}\frac{Pi}{Po}\)

\(\displaystyle 10^1=\frac{Po}{Pi}\)

\(Po=Pi\times10\)

題意より、\(Pi=24\)［mW］であるため、代入すると、

\(Po=24\times10=240\) ［mW］

となります。

次に回路上、変成器がありますが、電力は変成器で影響を受けない（変圧比が2の場合、電圧は倍になりますが、電流は半分になるためP=VIより電力は変わらない）ため、そのまま240［mW］が変成器より出力されます。

抵抗\(R_1\)で消費される電力\(P_1\) ［mW］は、抵抗\(R_1\)と\(R_2\)の比率が1:1のため、半分になります。

従い、

\(\displaystyle P_1=240\times\frac{1}{2}=120\)［mW］

となります。

（2）

問題

解説

解：2

特性インピーダンス\(Z_0\)の近似式は以下の通りですが、本問は暗記でよいでしょう。

\(\displaystyle Z_0\approx\sqrt{\frac{R}{j\omega C}}\)

\(\omega =2\pi f\)より、特性インピーダンス\(Z_0\)は、

\(\displaystyle Z_0\approx\sqrt{\frac{R}{j2\pi C}}\)

となるため、周波数の平方根と静電容量の平方根に反比例し、導体抵抗の平方根に比例となります。

（3）

問題

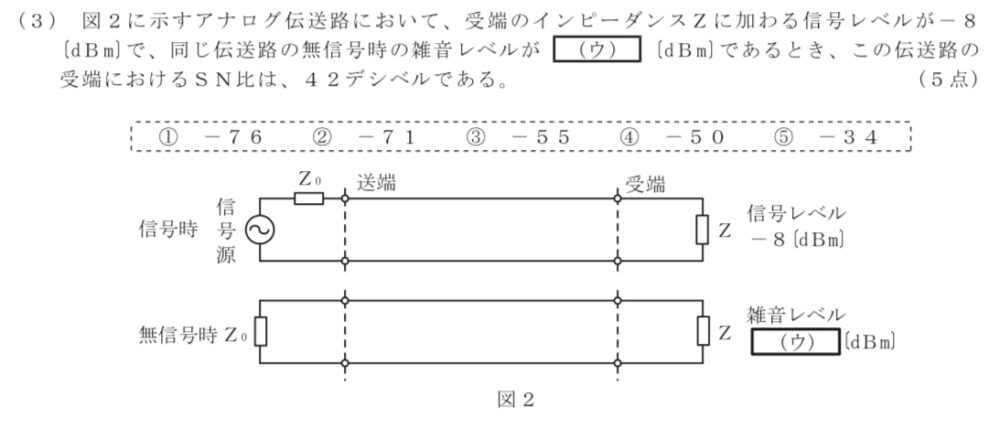
解説

解：4

S/N比とは、信号とノイズの比率を表すもので、信号の中にどれだけノイズが混入しているかを示しています。S/N比は、ノイズ電力\(P_N\)に対する信号電力\(P_S\)の比を対数で表します。

\(\displaystyle S/N比=10\log_{10}\frac{P_S}{P_N}\)

設問では、各電力が［W］では無く、［dBm］で与えられていますので注意が必要です。つまり、上記の式を対数の性質を利用し変換し、

\(S/N比=10\log_{10}{P_S}-10\log_{10}{P_N}\)

この式から、

\(10\log_{10}{P_S}\)は、信号電力を［dBm］で表したもの、\(10\log_{10}{P_N}\)はノイズ電力を［dBm］で表したものになります。

以上より、題意で与えられた値を代入すると、

\(42=-8-P_N\)

\(P_N=-50\)［dBm］となります。

（4）

問題

解説

解：1

電圧反射係数\(m\)とは、入力電圧\(V_i\)に対する反射電圧\(V_l\)の比率となります。電流反射係数\(n\)も同様の考えです。

負荷インピーダンスを\(Z\)、特性インピーダンスを\(Z_0\)とすると、\(m\)と\(n\)は以下の式で表せます。

電圧反射係数\(\displaystyle m=\frac{V_l}{V_i}=\frac{Z-Z_0}{Z+Z_0}\)

電流反射係数\(\displaystyle n=\frac{I_l}{I_i}=\frac{Z_0-Z}{Z+Z_0}\)

電流反射係数\(n\)を以下のように変形します。

\(\displaystyle n=-\frac{Z-Z_0}{Z+Z_0}\)

\(\displaystyle m=\frac{Z-Z_0}{Z+Z_0}\)であるため、代入すると、

電流反射係数\(n=-m\)となります。